Cross-Validation in sgdnet

Model validation is essential to both assess the performance¹ of a model and to be able to tune its parameters. sgdnet fits regularized models that are designed to avoid over-fitting. This, however, can only be accomplished if we split our data into training and test sets and tune our model by varying its parameters – in our case these is the regularization strength (\(\lambda\)) and the elastic net mixing parameter (\(\alpha\)) – and repeatedly fit our model against a training set and measure its performance against a test set.

There is a plethora of methods for model tuning. For sgdnet we have chosen to use \(k\)-fold cross-validation, which is available via the cv_sgdnet() function. This function will randomly divide the data into \(k\) folds. For each fold, the remaining \(k-1\) will be used to train a model across a regularization path, and optionally a range of \(\alpha\) (elastic net mixing parameters). The fold that is left out is then used to measure the performance of the model. We proceed across all the folds, which means that each observation is used exactly once for validation, and finally average our results across all the folds.

The end result is a tuned model with values for \(\lambda\) and \(\alpha\) chosen in a principled manner. We provide both \(\lambda_{min}\), which represents the model with the best performance and \(\lambda_{1SE}\), which gives the model with the largest \(\lambda\) with an error within one standard deviation of that of the best model; choosing this \(\lambda\) is often appropriate when the aim is to also achieve feature selection, because it often leads to a sparser model with only slightly worse performance. This is obviously not of value if \(\alpha = 0\) so that the ridge penalty is in place and no coefficient will be sparse.

We’ll illustrate the cross-validation feature in sgdnet using the heart data set, where the aim is to classify a person as having or not having heart disease. In this case, we’ll also keep a separate validation set for a final performance check. First we’ll set up these sets.

library(sgdnet)
library(Matrix)

set.seed(1)
train_ind <- ceiling(runif(270, 0, 270))
x_training <- heart$x[train_ind, ]
y_training <- heart$y[train_ind]
x_validation <- heart$x[-train_ind, ]
y_validation <- heart$y[-train_ind]

Next, we’ll use cv_sgdnet() to cross-validate and tune our model. We’ll try a range of elastic net penalties here and tune the model using misclassification error, by using type.measure = "class" in our call.

fit <- cv_sgdnet(x_training, 
                 y_training,
                 family = "binomial",
                 type.measure = "class",
                 alpha = seq(0.1, 0.9, by = 0.1))
plot(fit)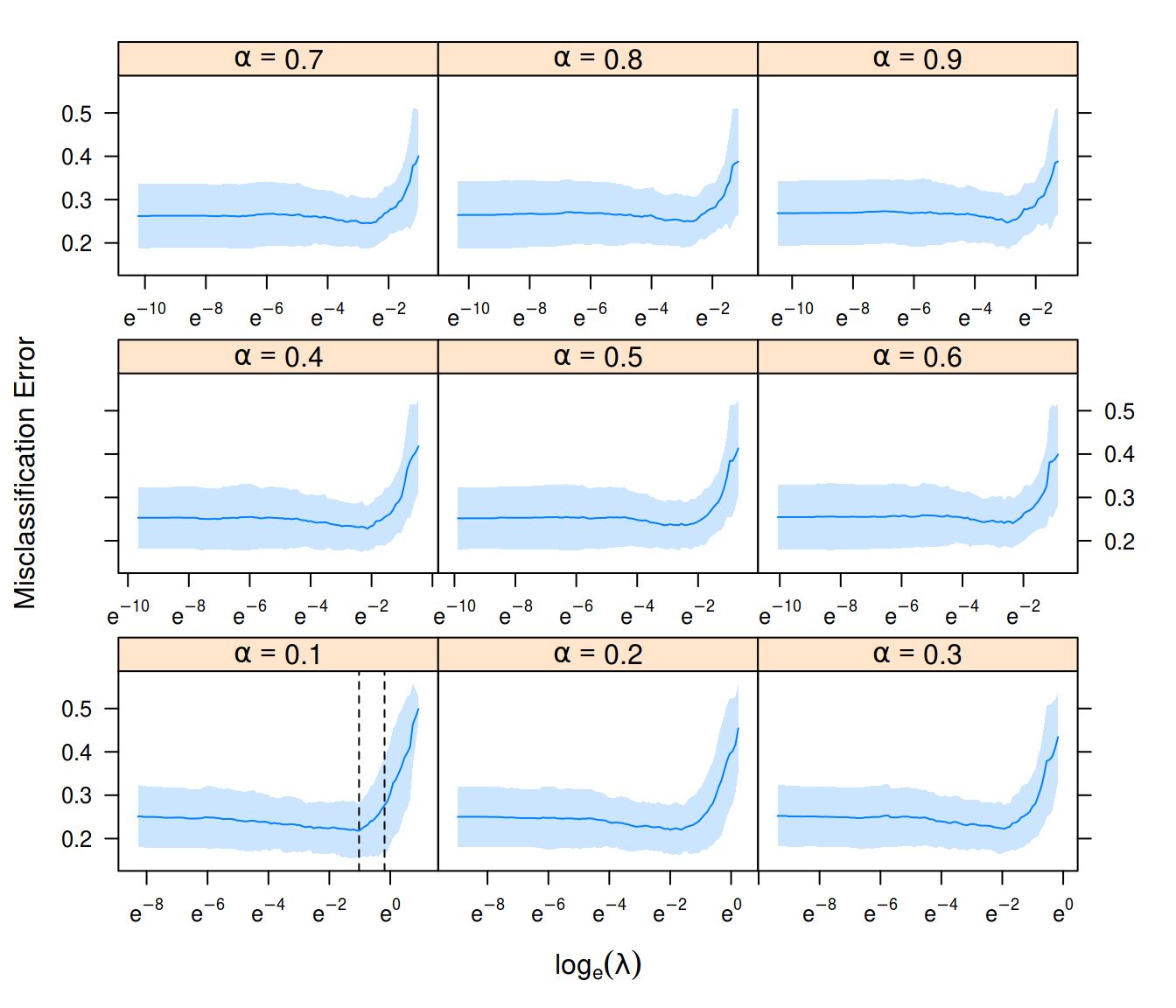

Results from model tuning using cv_sgdnet().

Our fit object also returns the model fit to the \(\alpha\) with the best performance, here \(\alpha = 0.1\). We can now use this model together with the \(\lambda\) corresponding to the best model, \(\lambda = 0.36\) to make predictions on the validation data set we left out at the start. There is a dedicated method for predict() for this, which is largely there to make it convenient to predict based on the tuned \(\alpha\) and \(\lambda\).

predicted_classes <- predict(fit, x_validation, "lambda_min", "class")

We could of course use the results from predict() to measure the performance on the validation set. sgdnet, however, features a shortcut for this via the score() function. For instance, the misclassification error for our validation set is then

score(fit, x_validation, y_validation, s = "lambda_min", type.measure = "class")
#>         1 
#> 0.1730769

In truth, cross-validation does not provide a measure of test error in the strict sense but rather a decent approximation of it, which may be particularly useful if the data set analyzed is small.↩

Johan Larsson

2018-08-13